Shannon en Weaver – A woven web of guesses

Ogenschijnlijk ben ik op een van die historische zijpaden terechtgekomen die ik -uit nieuwsgierigheid- graag bewandel. Deze keer echter, verwacht ik ook een aantal concepten en grondslagen tegen te komen die hun geldigheid nog niet verloren hebben, op het gebied van AI.

Wat vooraf ging: ik ben aan mijn huidige omzwerving begonnen toen ik bij Friston cs in het boek Active Inference een op het oog achteloos opgeschreven gebruik tegenkwam van “‘surprise‘ als de negatieve logaritme van een kans, met als eenheid de bit“. Dat pakketje concepten en hulpmiddelen ben ik uit elkaar aan het halen. Over het nut van de logaritme in het algemeen schreef ik hier, en over het gebruik van de logaritme bij bepalen van een maat voor informatie ging het in dit bericht.
Over de betekenis van kans (en kansverdeling) in deze context, in combinatie met verrassing (en onzekerheid), ga ik het nu hebben.

We gaan naar 1948/49. Terugkijkend vind je daar een landmark in de wetenschapsgeschiedenis, het beginpunt van wat tegenwoordig informatietheorie heet. Een theorie met ongekende impact op de wetenschappelijke en technische ontwikkelingen van de afgelopen decennia, en daardoor ook op alledaagse levens. De Magna Carta van het Informatietijdperk, zoals het door Scientific American is genoemd.

In 1949 verschijnt bij de University of Illinois een boekje, een bundel eigenlijk, met twee artikelen. Het eerste is van Warren Weaver en heet Recent Contributions to the Mathematical Theory of Communication. Het tweede is van Claude Shannon met de titel The Mathematical Theory of Communication. Dat is gelijk ook de titel van de bundel zelf.

De bundel uit 1949

Claude Shannon

Warren Weaver

Het artikel van Shannon is de feitelijke landmark, maar dat werd in die tijd niet onmiddellijk zo gezien. Het was in 1948 al gepubliceerd in Bell System Technical Journal, waarmee het niet veel aandacht trok, al helemaal niet bij een breder publiek dan ingenieurs en technici. Het is voor die tijd wellicht te moeilijk, te conceptueel en voor technici te wiskundig en voor wiskundigen te technisch. Warren Weaver, destijds natuurwetenschappelijk directeur van de Rockefeller Foundation, ziet wel meteen het belang van het werk van Shannon. Het artikel van Weaver in de bundel is een oorspronkelijk voor Scientific American geschreven niet al te technisch artikel waarin de inhoud van Shannon’s werk op waarde wordt geschat en uitgelegd in niet-technische termen.

NB Interessant is dat de titel van Shannon’s artikel in het Bell System tijdschrift begint met “A Mathematical Theory …”, een jaar later begint de titel van het (verder ongewijzigde) artikel in de bundel met “The Mathematical Theory …”. Ik waag mij niet aan duiding van het verschil.

Ik heb beide artikelen gelezen en voor het grootste deel begrepen, denk ik zelf. Ik vond ze opvallend ‘modern’, qua stijl en taalgebruik, maar ook de inhoud doet wonderlijk genoeg niet ouderwets aan. Het zegt iets over de hoge kwaliteit en tijdloosheid van de ideeën en concepten. Bedenk dat bijvoorbeeld de transistor nog niet was uitgevonden en dat dit nog de tijd is van relais om te schakelen ten behoeve van telegrafie en telefonie, telex, teletype.

Hieronder volg ik inhoudelijk de artikelen van Shannon en Weaver, tot en met de formulering van wat later de Shannon entropie is gaan heten, een maat voor informatie en voor onzekerheid, verrassing. In de titels van beide artikelen is (nog) sprake van Communication, maar in de tekst komt al snel het concept Information naar voren. Het is de kern van het werk van Shannon en de reden dat we het vakgebied Informatietheorie zijn gaan noemen.

Shannon-Weaver model

Weaver benoemt in zijn artikel drie probleemgebieden bij het onderwerp communicatie, levels noemt hij ze.

A. Het technische probleemgebied: hoe accuraat kunnen symbolen in communicatie worden verzonden?
B. Het semantische probleem gebied: Hoe nauwkeurig brengen de verzonden symbolen de gewenste bedoeling over?
C. Het effectiviteitsprobleem: Hoe effectief beïnvloedt de ontvangen bedoeling het gedrag van de ontvanger?

Shannon, in zijn artikel, heeft dan al hardvochtig afscheid genomen van de gebieden B. en C. door te stellen dat de semantische aspecten van communicatie irrelevant zijn (zijn woorden) voor het ‘engineering problem‘, ook al hebben berichten vaak een inhoudelijke lading.

De probleemstelling van Shannon, de onderzoeksvraag, is:

“The fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point”.

Shannon refereert aan eerder werk van Ralph Hartley dat hier aan de orde was. De semantische aspecten vallen bij Hartley in de categorie psychologische factoren die voor het ontwikkelen van een maat voor informatie niet van belang zijn en die hij ook zo snel mogelijk kwijt wil.

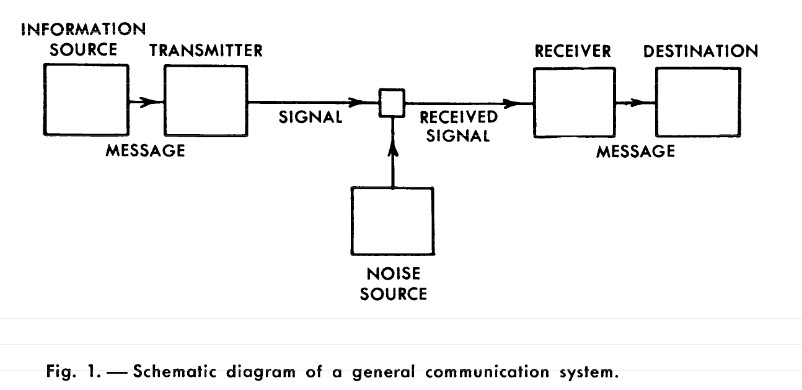
Daar waar Hartley zich bezighield met de verzending van berichten en op zoek was naar een maat voor de omvang ervan, richt Shannon zich vooral ook op het punt waar berichten landen, in de samenhang van een general communication system. Het one point en another point uit de probleemstelling plaatst hij aan begin en einde van een schema dat tegenwoordig bekend staat als Shannon-Weaver model of Shannon model.

In het schema zijn Transmitter en Receiver, en hun verbinding Channel, technische componenten die berichten omzetten in signalen (of andersom) en de transmissie van signalen en het opvangen ervan mogelijk maken.
De Information source produceert een bericht, of een sequentie berichten. Berichten zijn er in verschillende types, variërend van een serie letters zoals bij telegraaf of telex tot tijdgerelateerde functies in een driedimensionaal continuüm, zoals bij televisie.
De Destination is een persoon of een ding waarvoor het bericht bedoeld is.

Het is buiten scope om de theorie hier verder uit te werken, maar van belang in het schema is het element Noise (ruis), een door Shannon ingebrachte nieuwigheid. Ruis is het fenomeen dat een eenmaal verzonden bericht niet ongehinderd en onveranderd aankomt bij de bestemming, door allerlei mogelijke oorzaken. Ruis zelf was uiteraard geen nieuw fenomeen, integendeel, het was de nachtmerrie van telegrafie en telefonie operators.

Het nieuwe is dat Shannon ruis integraal als een gelijkwaardig element opneemt in het communicatie systeem. Soms is ruis onbedoeld en hinderlijk, in andere gevallen juist bedoeld en nuttig. Je zou kunnen zeggen dat ‘bedoelde ruis’ in de oorlogsjaren zelfs de core business van Shannon was. Bij Bell Labs hield hij zich bezig met het ontwerp van telefonie systemen waarbij het signaal met opzet zodanig wordt vervormd dat het voor derden niet te ontcijferen is. Te gebruiken door Roosevelt en Churchill voor strategisch overleg zeg maar.

Het concept informatie

En passant, met het schema, is het begrip informatie naar voren gekomen. Weaver waarschuwt voor verwarring:

Het woord ‘informatie’, in deze theorie, wordt in een speciale betekenis gebruikt en moet niet verward worden met het gewone gebruik. In het bijzonder moet ‘informatie’ niet worden verward met betekenis.

En:

Bij informatie in de communicatieleer gaat het niet zozeer om wat je overbrengt, maar om wat je zou kunnen overbrengen.

Shannon heeft het over ‘message selected‘. Dit is volgens mij een kernpunt van het artikel: we laten de semantiek vallen, maar in het besef dat een bericht altijd is geselecteerd uit een verzameling mogelijke berichten.

Logaritmische maat

Net als bij Hartley is de ontwerpoverweging bij een communicatie systeem dat het alle mogelijke selecties moet kunnen faciliteren, en net als Hartley kiest Shannon voor de logaritmische maat uit praktische overwegingen. Parameters bij het ontwerp zoals bandbreedte, of aantallen relais (we zijn nog in de jaren 40 van de vorige eeuw) variëren lineair met de logaritme van het aantal mogelijkheden. En het is intuïtiever. Stel je hebt een ponskaart met posities voor 2 gaten overeenkomend met een 0 voor geen gat en een 1 voor wel een ponsgat. Er zijn 4 mogelijke combinaties (00, 01, 10, 11), $2^2$ . Als we overgaan naar ponskaarten met 4 posities zegt je intuïtie dat de capaciteit is verdubbeld (van 2 naar 4 immers). Maar het aantal combinaties is $2^4$ , dat wil zeggen dat er 16 mogelijke combinaties zijn, in werkelijkheid is de capaciteit verviervoudigd.
Van exponentieel naar lineair, dat is wat de logaritme voor je doet.

Eenheid van informatie: de bit

De maat voor informatie is dus een logaritme, maar wat is dan de eenheid, waar meten we in? Het is makkelijk in te zien, zie ook eerdere berichten, dat de eenheid afhangt van het gekozen grondtal voor de logaritme. Shannon kies voor grondtal 2, en komt zo tot binary digits, oftewel bits. Een relais (open/dicht) of een flipflop schakelelement kan dan 1 bit informatie opslaan. Hoewel het woord ‘bit’ oorspronkelijk elders is bedacht (door J.W. Tukey), wordt de introductie van de bit als eenheid van informatie meestal aan Shannon toegeschreven. Dat concept is niet meer weggegaan…

Discrete informatiebron als stochastisch proces

Communicatie systemen zijn er grofweg in drie smaken: discrete, continue en gemengde. Discreet wil zeggen dat zowel het bericht als het signaal sequenties zijn van apart te onderscheiden symbolen, denk aan letters en cijfers of de punt en streep van het Morse alfabet. In het continue geval gaat het om continue functies, zoals bij radio(golven). Shannon werkt vooral de discrete situatie uit, ook als basis voor de continue systemen. Hij zegt er bij dat het in eerste instantie om communicatiesystemen gaat, maar dat de toepassing algemene(re) geldigheid heeft zoals bij computersystemen, telefonie en andere gebieden.

Bij discrete informatiebronnen wordt een bericht symbool voor symbool samengesteld, waarbij de keuze voor een symbool steeds een zekere waarschijnlijkheid heeft. Een model of systeem dat zo werkt heet een stochastisch proces. Omgekeerd is elk stochastisch proces dat sequenties van onderscheiden symbolen uit een eindige verzameling samenstelt te beschouwen als een discrete informatiebron.

NB Stochastisch wordt hier gebruikt om het proces te onderscheiden van een deterministisch proces, waarbij elke keuze op voorhand vastligt en van een random proces, waarbij de samenstelling van berichten volstrekt willekeurig en onherhaalbaar is.

Ik sla een paar stappen van Shannon over, maar zoom nog even in op zijn conclusie dat de keuze van een volgend symbool probabilistisch van aard is, maar dat er niet altijd sprake is van een onafhankelijke kans.

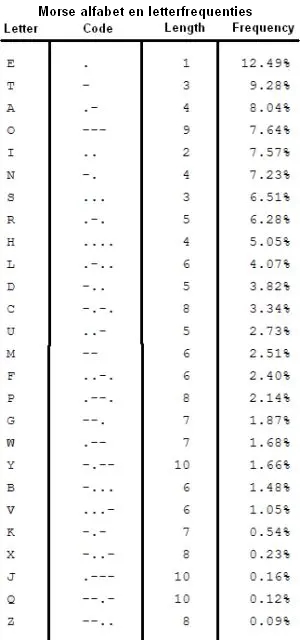
De letters uit een alfabet komen met verschillende frequentie in de taal voor. In het Engels bijvoorbeeld is de frequentie van de letter E 12%, van de W maar 2%. Het Morse alfabet hield van oudsher (vanaf 1837) al rekening met die letterfrequenties, daarom vertegenwoordigt het eenvoudigste Morse symbool, de punt ., de letter E. De T is tweede met 9% in de frequentielijst en wordt weergegeven met een enkele Morse-streep -. Voor de W zijn al 3 symbolen nodig: . – –

Bedenk: bij een standaardsnelheid van 12 woorden per minuut wordt de morsesleutel bij een punt ongeveer 0,1 seconde ingedrukt, bij een streep 3x zo lang. De tussenruimte tussen tekens is ook 0,1 seconde, de tijd tussen letters 0,3 seconde en de tijd tussen woorden 0,7 seconde

Sommige combinaties van letters zijn veel (on)waarschijnlijker dan andere. In de praktijk wordt de keuze van een letter soms bepaald door de voorgaande letter. In het Engels komt TH veel vaker voor dan XP, in het Nederlands wordt een C vaak gevolgd door een H.
Je zou zelfs nog verder kunnen kijken, tot 3 letters. THE of THO komen vaak voor als er al TH staat, in het Nederlands vaak SCH als er eenmaal sprake is van SC.

Shannon spreekt van een nulde-orde benadering voor (de keuze van) een willekeurige letter, een eerste-orde benadering als we rekening houden met letterfrequenties, een tweede-orde benadering voor de twee letter combinaties, en van derde-orde bij de drie letters.

In theorie zou je zo door kunnen gaan, maar volgens Shannon is het dan slimmer om niet op letters te focussen, maar op woorden zoals ze in een taal bestaan. Ook daar zijn frequenties van voorkomen en van combinaties beschikbaar en kun je dezelfde benadering kiezen met eerste-orde op basis van woordfrequenties, en tweede-orde benadering gebaseerd op gangbare combinaties.

Markov processen

De hier beschreven stochastische processen staan in de wiskunde bekend als discrete Markov processen. Ze komen bij Friston cs in hun werk over Active Inference in die vorm terug, maar in andere vorm ook al veel eerder – vanaf de jaren 80 bijvoorbeeld als Hidden Markov Models (HMM) in onderzoek rond spraakherkenning, of als Markov Decision processes (MDP) in de operations research. In 1988 verschijnt van de hand van Judea Pearl Probalistic Reasoning in Intelligent Systems. Daar spelen ze een rol bij de modellering van onafhankelijkheidsrelaties tussen stochastische variabelen.

Een Markov proces is een model dat een reeks mogelijke gebeurtenissen (‘events’) beschrijft, waarbij de kans op een gebeurtenis alleen afhangt van de huidige toestand, ongeacht wat er voorafgegaan is.

Shannon omschrijft het formeler als:

Een model van een systeem met een eindig aantal mogelijke toestanden (‘states‘) $S_1, S_2, S_3, ...., S_n$ en een verzameling kansen $p_i(j)$ dat toestand $S_i$ over zal gaan in toestand $S_j$ . Zo’n Markov proces is een informatiebron, bijvoorbeeld onder de aanname dat er bij elke overgang een letter wordt geproduceerd.

Het concept “Hoeveelheid informatie”

Kun je nu, in het geval van een discrete informatiebron als Markov proces, iets zeggen over hoeveel informatie er wordt “geproduceerd” door zo’n proces? Ik volg de tekst van Shannon:

Stel we hebben een set mogelijke gebeurtenissen waarvan de kansen dat ze optreden $p_1, p_2, ..., p_n$ zijn. De kansen zijn bekend, maar dat is alles wat we weten over welke gebeurtenis zal plaatsvinden. Kunnen we een maat vinden voor de hoeveelheid ‘keuze’ (“choice”) bij de selectie van een gebeurtenis, of van de mate van onzekerheid over de uitkomst?

Als er zo’n maat is, laten we zeggen $H(p_1, p_2,...,p_n)$ dan moet die redelijkerwijs de volgende eigenschappen hebben:

$H$ moet continu zijn in de $p_i$ .

Als alle $p_i$ gelijk zijn, $p_i=\frac{1}{n}$ , dan moet $H$ een monotoon stijgende functie van $n$ zijn. Als gebeurtenissen even waarschijnlijk zijn neemt de keuze, of onzekerheid, toe naarmate er meer mogelijke gebeurtenissen zijn.

Als een keuze uiteen kan vallen in twee opvolgende keuzes, dan moet de originele $H$ gelijk zijn aan de gewogen som van individuele waarden van $H$ .

Daarna formuleert Shannon een impactrijke stelling:

De enige $H$ die aan alle drie voorwaarden voldoet is van de vorm:
$H=-K\sum_{i=1}^{n}p_ilogp_i$
waarbij K een positieve constante is.

Ter herinnering: omdat de $p_i$ altijd getallen tussen 0 en 1 zijn, is de logaritme ervan negatief, de sommatie dus ook. Met het min-teken voor het geheel is $H$ dus altijd positief.

De afleiding van de formule geeft Shannon in Appendix 2 bij het artikel. Materieel gezien is die hetzelfde als bij Hartley, met één uitbreiding: Hartley gaat uit van gelijke waarschijnlijkheid van de te maken keuzes (eigenschap 2.) en heeft dan aan het aantal mogelijkheden en de lengte van het bericht genoeg. Bij Shannon hoeft de kansverdeling niet uniform te zijn, en mogen de $p_i$ zelfs irrationeel zijn. De eigenschappen van continuïteit en gewogen additiviteit (1. resp. 3.) geven de formule dan zijn algemene geldigheid.

In algemenere vorm is deze formule beslist T-shirt waardig:

$H(X)=-\sum_{i=1}^{n}p(x_i)logp(x_i)$

Dit is de Shannon entropie. Bij grondtal 2 voor de logaritme wordt $H$ uitgedrukt in bits.

In een volgend bericht ga ik in op de Shannon entropie en de relatie met onzekerheid en verrassing, dat is voor mij voldoende om weer te kunnen invoegen op het pad naar Active Inference.

In zijn artikel gaat Shannon zelf veel verder. Een belangrijk resultaat is de uitwerking van het concept kanaalcapaciteit. Shannon toont aan dat er een maximum is aan de hoeveelheid informatie die kan worden verzonden via een kanaal met ruis: dit is een theoretische bovengrens, de later zo genoemde Shannon limiet. In het artikel laat hij zien dat het mogelijk is informatie foutloos te verzenden over een kanaal met ruis, zolang de transmissiesnelheid lager is dan de kanaalcapaciteit. Verder komen de mogelijkheden van zg. broncodering aan de orde, die uiteindelijk de basis is van datacompressie. Shannon laat zien dat een bron met een bepaalde entropiesnelheid gecomprimeerd kan worden tot die snelheid zonder verlies van informatie.