De formule van Bayes
De Stelling van Bayes wordt vaak uitgedrukt in een formule die mooi genoeg is om op een T-shirt te zetten. Om te begrijpen wat er staat is wel wat uitleg nodig, die staat in dit bericht.
Eerder ging het over de situatie dat je in een medische test een positieve uitslag hebt gekregen die aangeeft dat je mogelijk een bepaalde ziekte hebt opgelopen. Als je dat weet, wat is dan de kans dat je de ziekte daadwerkelijk hebt?
Die situatie gebruik ik voor de afleiding van de formule van Bayes:
![]()
Mijn uitleg is visueel, met Venndiagrammen. Daarna laat ik zien hoe de formule bepaald kan worden. Een berekening met getallen uit het eerdere voorbeeld laat zien hoe de formule in de praktijk werkt. Tot slot een voorbeeld van Bayesiaans denken aan de hand van hetzelfde voorbeeld.
NB De uitleg is geïnspireerd op diverse bronnen op het internet, ik heb het meest gebruik gemaakt van een artikel van Oscar Bonilla: Visualizing Bayes Theorem. De plaatjes heb ik zelf gemaakt, maar komen inhoudelijk overeen met die uit het artikel.
Venndiagrammen
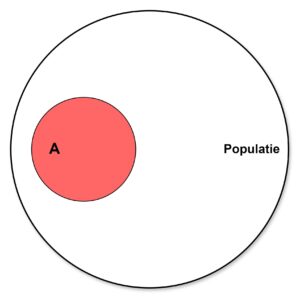
Dit is het Venndiagram van de situatie in het vorige bericht: in een gegeven populatie komt de ziekte A voor.
De cirkels vertegenwoordigen de (aantallen) personen die het betreft. De cirkel A betreft de aantallen personen die de ziekte hebben.
De kans dat een willekeurig gekozen persoon uit de populatie Po de ziekte A heeft opgelopen is als formule te schrijven:
![]()
Formule 1
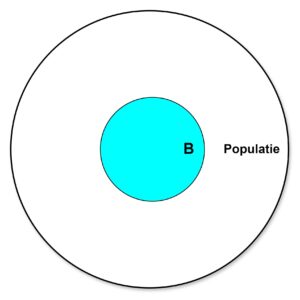
Op dezelfde manier geven we de groep aan met een positieve uitslag bij de medische diagnose test op de ziekte.
De cirkel B betreft de aantallen personen in de populatie die positief zijn getest.
De kans dat een willekeurig gekozen persoon uit Po positief is getest op de ziekte is in formule:
![]()
Formule 2
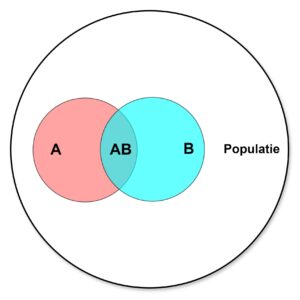
Door beide plaatjes samen te voegen kun je zien welk deel van de populatie de ziekte heeft (A), welk deel positief getest is (B) en -op de doorsnede- welk deel positief is getest en ook daadwerkelijk de ziekte heeft opgelopen: ![]() , we schrijven het hier als AB.
, we schrijven het hier als AB.
Net als in de andere situaties is de kans dat een willekeurig gekozen persoon én ziek én positief getest is in formule vorm te schrijven:
![]()
Formule 3
NB De P van P(A) staat voor probabiliteit (de kans op A). Met de | | geven we aan dat het om de aantallen in de betreffende verzameling gaat. Po wordt vaak Universum genoemd.
In het samengevoegde plaatje bevinden zich in het rode deel degenen die wel ziek zijn maar niet positief getest, in het blauwe deel degenen die wel positief testen maar de ziekte niet hebben en in het overlappende deel diegenen die de ziekte hebben én positief testen.
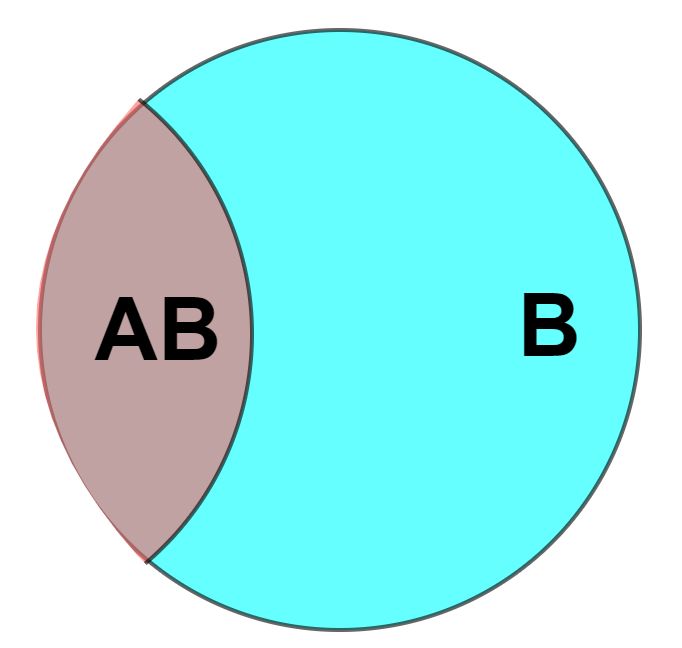
We zoomen in op het blauwe deel van het diagram. Daar waar we voor het grotere geheel spreken over de populatie Po, zou je voor dit deel kunnen spreken over de populatie B (alle positief getesten). Net zoals we hierboven voor A binnen de populatie Po, en B binnen de populatie Po, iets konden zeggen over de probabiliteit kunnen we dat nu over de probabiliteit van tegelijkertijd A en B (AB) binnen de (ingezoomde) populatie B.
Formules uitwerken en samenvoegen
In de vier formules staan nog de echte aantallen van de populatie. Met eenvoudige wiskunde kunnen we die elimineren en de formule opbouwen met alleen waarschijnlijkheden erin – die staan los van de populatie omvang. Het gaat als volgt.
Formule 3 hierboven kunnen we schrijven als ![]() .
.
En formule 2 als ![]() .
.
We vullen beide in, in formule 4: ![]()
Deel boven en onder door |Po|, en voila we zijn de aantallen kwijt in de formule en houden over:
![]()
Nog één stap. De situatie zoals we die hebben uitgewerkt betreft de kans dat een persoon ziek is (dus onderdeel van A), wetende dat hij positief getest is (dus onderdeel van B).
Door in de formules A en B te verwisselen zeggen we iets over de kans dat iemand positief test, wetende dat hij ziek is:
![]()
In de laatste twee formules kunnen we P(AB) elimineren, zoals we dat hierboven met |Po| deden, dan komt er:
![]()
Dat is eigenlijk al de formule van Bayes, in volle schoonheid vanwege de in het oog springende symmetrie.
Vanwege de interesse in
![]()
Rekenvoorbeeld
Hoe pas je de formule toe? Ik laat het zien aan de hand van de casus uit het vorige bericht.
Dit zijn de gegevens:
- In de populatie waar we naar kijken gaat een ziekte rond, met een besmettingsgraad van 0,1%
- Er is een medische diagnose test met een betrouwbaarheid van 99%, dat wil zeggen dat van alle positief geteste mensen 99% de ziekte ook echt heeft, 1% komt wel positief uit de test maar heeft de ziekte niet.
- Jij bent positief getest, dat wil zeggen dat de test aangeeft dat je waarschijnlijk de ziekte hebt.
Wat is, vanuit Bayesiaans perspectief, nu de werkelijke kans dat je de ziekte hebt?
We hebben voldoende data om de formule van Bayes te kunnen toepassen, te kunnen invullen. Laten we met A het hebben van de ziekte aangeven, met B de positieve test. We willen weten wat de kans is dat je de ziekte hebt, wetende dat je positief getest bent – dat is ![]() in de termen van hierboven, de onbekende zeg maar. Weten we wel wat de waarde van de andere termen in de formule is?
in de termen van hierboven, de onbekende zeg maar. Weten we wel wat de waarde van de andere termen in de formule is?
![]()
- Boven de streep weten we dat
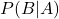 de (voorwaardelijke) kans is positief getest te worden als je de ziekte hebt. Die kans is in deze casus 99% (de betrouwbaarheid van de test).
de (voorwaardelijke) kans is positief getest te worden als je de ziekte hebt. Die kans is in deze casus 99% (de betrouwbaarheid van de test). - Ook boven de streep staat
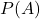 , de (a priori) kans om de ziekte te hebben. Gegeven de besmettingsgraad kunnen we deze gelijk stellen aan 0,1%
, de (a priori) kans om de ziekte te hebben. Gegeven de besmettingsgraad kunnen we deze gelijk stellen aan 0,1% - Onder de streep staat
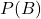 voor de kans dat je positief getest wordt. Die heeft twee componenten: een positieve test terwijl je de ziekte hebt – gelijk aan
voor de kans dat je positief getest wordt. Die heeft twee componenten: een positieve test terwijl je de ziekte hebt – gelijk aan 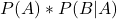 (dat is 0,1 % x 99%) – , en een positieve test terwijl je de ziekte niet hebt – gelijk aan
(dat is 0,1 % x 99%) – , en een positieve test terwijl je de ziekte niet hebt – gelijk aan 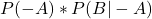 (dat is 99,9% x 1%).
(dat is 99,9% x 1%).
Alles netjes ingevuld levert:
![]()
In procenten is de kans dat je de ziekte werkelijk hebt opgelopen volgens de regel van Bayes circa 9%, overeenkomend met de ‘grafische’ oplossing uit het vorige bericht.
Bayesiaans denken
In vorige en komende berichten op deze site is er volop aandacht voor wat wel Bayesiaans denken wordt genoemd. In deze paragraaf alvast een kernelement uit die manier van denken, geïllustreerd aan het uitgewerkte voorbeeld.
Bayesiaans denken wordt gekenmerkt door wat in essentie een subjectieve benadering is.
- Je hebt een idee, een overtuiging, over de buitenwereld, en over de situatie die aan de orde is. In het jargon spreekt men van belief.
- Dat belief is gebaseerd op een (eerste) aanname, een a priori waarschijnlijkheid, in het jargon kortweg de prior.
- Perceptie van de buitenwereld brengt je tot gevolgtrekking(en), inferentie (inference).
- Het kan nodig zijn op basis van de inferentie je belief bij te stellen tot een nieuwe, a posteriori, waarschijnlijkheid, de posterior.
- In (altijd) veranderende omstandigheden zal je nieuwe belief weer tot nieuwe inferentie leiden, waarbij de verkregen posterior je nieuwe prior waarschijnlijkheid wordt en de gang van zaken zich herhaalt.
Zo bouwt de Bayesiaan zijn beeld van de werkelijkheid op, in een cyclus van nieuwe laagjes.
Wat is in ons voorbeeld van de ziekte en de diagnose test de prior? Dat is de aanname over de initiële kans om de ziekte te hebben, gebaseerd op de besmettingsgraad. In het rekenvoorbeeld is die 0,1 %.
De stelling van Bayes geeft ons via de formule de posterior. Dat is de waarschijnlijkheid dat je de ziekte hebt, wetende dat je positief getest bent. In het rekenvoorbeeld komt die op circa 9%.
Stel dat je na de eerste diagnose test voor de zekerheid de test opnieuw laat afnemen. Au, de uitkomst is weer positief. Ook nu stellen we de vraag wat de kans is dat je daadwerkelijk de ziekte hebt.
De formule blijft dezelfde, maar in je nieuwe belief krijgt de prior ![]() een andere waarde, namelijk die van de posterior uit de eerste laag, te weten 9%. Ingevuld wordt dat:
een andere waarde, namelijk die van de posterior uit de eerste laag, te weten 9%. Ingevuld wordt dat:
![]()
Je nieuwe posterior, de kans om na twéé positieve testen daadwerkelijk de ziekte te hebben, is bijna 91%. Een groot verschil met de eerste 9%, maar nog steeds niet de 99% van de betrouwbaarheid van de test.
Tot slot van dit bericht een wellicht wat wonderlijke vraag. Dacht Bayes zelf Bayesiaans? Het antwoord wil ik in de ontstaansgeschiedenis van de stelling van Bayes proberen te vinden – in een volgend bericht.