Sneeuw – A woven web of guesses

Als je tv zit te kijken en de zender valt door een storing weg, dan laat je beeldscherm ruis zien, sneeuw. Eerst ben je verrast, maar nadat je eenmaal hebt geconstateerd dat de zender weg is ben je al snel verveeld, je kunt niet wachten tot de storing is verholpen.

Vanuit informatietheoretisch oogpunt is dat vreemd, elk nieuw frame met sneeuw heeft telkens een maximale informatie-inhoud – entropie in Shannon termen – omdat het volledig onvoorspelbaar is. Er is geen structuur of patroon te ontdekken, daardoor blijft de surprise theoretisch gezien constant hoog.

In de praktijk is de verrassing snel verdwenen omdat jouw brein zich heel snel een nieuw model vormt van wat het waarneemt. Dat model zegt: het is ruis zonder betekenisvolle patronen, veroorzaakt door een onbekende storing, het wordt pas weer interessant als de storing verholpen is.
Dit is active inference in werking… het is er actief op uit de surprise te minimaliseren.

NB In moderne apparaten wordt het scherm met sneeuw meestal afgevangen door het toestel en krijg je een zwart scherm te zien.

Dit voorbeeld staat bekend als de white snow paradox (Itti 2009). Het laat goed zien dat naarmate een waarneming in een bepaalde situatie beter overeenkomt met de verwachting die je er van had je minder verrast zult zijn. Het levert je een soort bewijs dat de de waargenomen data in die situatie passen bij jouw overtuiging, bij jouw huidige model van de werkelijkheid.

Waarnemingen komen soms niet overeen met wat je verwachting is, maar wijken er in meer of mindere mate vanaf. Dat werpt de algemene vraag op: hoe goed worden de waarnemingen -door de bank genomen- verklaard door jouw model bij alle mogelijke waarden van de modelparameters? Het antwoord op die vraag zegt iets over de waarschijnlijkheid van het model zelf.

Als er voor veel parameters in je model afwijkingen zijn, moet je misschien jouw model inruilen voor een versie die beter de waargenomen data verklaart.

Kansverdelingen

Tot hier konden we het doen met min of meer alledaags taalgebruik, met de onzekerheden die daar misschien bij horen. Wat betekent ‘door de bank genomen’ in de alinea hierboven, hoe bepaal je dat waargenomen data ‘passen’ in je wereldbeeld? Hoe weet je of een ander model ‘beter’ de waarnemingen verklaart? Enzovoort.

Bij een verdere uitwerking ontkom ik niet aan formele definities en een meer technische uitleg van de theorie van active inference. Dit is gelijk het goede moment om los te komen van de individuele, enkelvoudige, voorbeelden en over te gaan naar de modelmatige manier van redeneren die ik in het vorige bericht al heb aangekondigd.

De modellen waar het hier over gaat, generatieve modellen, zijn modellen van hoe zintuiglijke waarnemingen worden voortgebracht door objecten en gebeurtenissen, ‘states‘, die je niet direct kunt kennen. Daarom noemden we ze in eerdere berichten hidden.

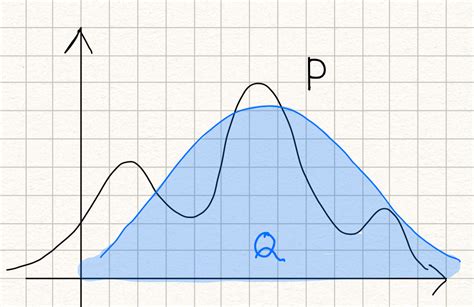
Zulke modellen zijn te beschouwen als kansverdelingen. Die zijn er in allerlei soorten en vormen. In de praktijk is een kansverdeling vaak grillig, de berekeningen weerbarstig of onoplosbaar (intractable). Zie ook de terechte opmerking van Cor de Beurs bij Surprise surprise. In het plaatje is $P$ zo’n verdeling.

Verdelingen met wiskundig gezien ‘interessante’ kenmerken zijn soms naar hun (vermeende) ontdekker genoemd – Gauss, Dirichlet, Cauchy, Poisson, Laplace, Maxwell-Boltzmann – of naar die kenmerken zelf – geometrisch, normaal, hypergeometrisch, logistisch, binomiaal. Dit zijn verdelingen waaraan wel succesvol gerekend kan worden. In het schetsje is $Q$ er zo een (een normaal verdeling in dit geval).

Surprise(s)

De overgang van individuele voorbeelden naar generatieve modellen raakt ook het concept surprise. We maken onderscheid tussen surprise bij een enkelvoudig waarneming en surprise bij een verzameling of reeks van waarnemingen. In de Bayesiaanse context is er nog een derde variant waarbij de waarnemingen in relatie met de prior worden beschouwd.

Enkelvoudige waarneming

De definitie van surprise $S$ bij een enkelvoudige waarneming $o$ met kans $P(o)$ is in formulevorm:

$S(o)=-logP(o)$

Deze vorm van surprise is de Shannon surprise. In de context van informatietheorie wordt dit meestal de informatie-inhoud of zelf-informatie genoemd en geschreven als $I(x) = -log(p(x))$

. De eenheid is bit als de logaritme grondtal 2 heeft. In het sneeuw op tv voorbeeld is die informatie-inhoud telkens maximaal omdat elke pixel willekeurig verandert.

Reeks waarnemingen

Het enkelvoudige voorbeeld kunnen we generaliseren naar een reeks waarnemingen en daarmee naar het generatieve model zelf. Als $D$ de volledige dataset van waarnemingen is en $x$ de parameters van het generatieve model zijn, dan is de gegeneraliseerde surprise $S$ :

$S(D)=-logP(D|x)$

Model evidence

In de casus van de springende appel die we eerder tegenkwamen op ons pad, de Low Road naar active inference, was er ook al sprake van verrassing, van surprise. In het voorbeeld gaf ik de formele definitie ervan die voor mij toen uit de lucht kwam vallen. Nu kan ik het beter plaatsen, al vergt het nog enige uitwerking. Dit is die definitie:

Surprise is de negatieve logaritme van de marginal likelihood.

In Bayesiaanse interpretatie is marginal likelihood de generalisatie van de waarneming bij alle mogelijke modelparameters, gecombineerd met de prior over die parameters. In de context van active inference wordt dit de model evidence genoemd.

De marginal likelihood bereken je door de waarschijnlijkheid van de waarneming -de likelihood op basis van de a priori overtuiging- te combineren met die prior, gesommeerd over alle mogelijke waarden van s.

$P(o) = \sum_s P(o|s)P(s)$

NB Zie de voorbeeldberekening in de situatie van slechts twee mogelijke waarden (i.c. appel of kikker) of het voorbeeld van de medische test waarbij de marginal likelihood gevormd wordt door alle positief getesten, de werkelijke ziektegevallen en de ‘false positives’ bij elkaar opgeteld.

De basis voor de Bayesiaanse benadering in het algemeen is de stelling van Bayes. De oervorm betreft een enkelvoudige waarneming, die al dan niet in overeenstemming is met de enkelvoudige prior $P(s)$ .

$P(s|o)=\frac{P(o|s)*P(s)}{P(o)}$

De marginal likelihood van de enkelvoudige situatie is de noemer in deze formule. Als het over generatieve modellen gaat worden deze enkelvoudige waarden in de sommatie over de modelparameters gebruikt om een soort gewogen gemiddelde uit te rekenen, dat is feitelijk de model evidence die bedoeld wordt.

$P(o)$ is de marginal likelihood, of – in dit geval veelzeggender: de model evidence.
$P(o|s)$ is de likelihood, de waarschijnlijkheid van wat je waarneemt gegeven je overtuiging
$P(s)$ is de prior, je initiële overtuiging
$P(s|o)$ is de posterior, de update van de prior

In het sneeuw op tv voorbeeld is de kans dat je ruis blijft zien gesommeerd over alle situaties waarin de storing niet verholpen is gelijk aan 1 (100%), conform jouw overtuiging over de aard van sneeuw op tv. $log(1)=0$ , dus de surprise is ook nul.

Berekenbaarheid

In de formele definitie is verrassing een getal (een aantal bits) waardoor we kunnen spreken over meer of minder verrassing, of: over een hogere of lager informatie-inhoud van het geheel van je waarnemingen.

Er is meer over dit onderwerp te zeggen in kwantitatieve zin. Als de theorie van active inference operationeel moet worden in daadwerkelijke kunstmatige intelligentie is dat ook nodig. Om planning en keuzes te kunnen maken moet een intelligent agent kansverdelingen met elkaar kunnen vergelijken, zoals de prior verdeling, de posterior-verdeling, en mogelijke benaderingen van posterior-verdelingen.

Om onoplosbaarheid (intractability) te omzeilen kwam ik verschillende suggesties tegen om de uitkomst zo goed mogelijk te benaderen of te schatten, zo nodig met steekproeven of simulatie.

Laplace-benadering
In deze methode wordt geprobeerd de posterior-verdeling te benaderen met een Gaussiaanse normaalverdeling is (dat is gelijk de beperking van de methode). Zo’n verdeling heeft een maximum, in het midden zeg maar. Zie ook het plaatje hierboven. De logaritme van de posterior is te benaderen met een functie rond dit maximum.
Monte Carlo-integratie en Nested sampling
Dit zijn numerieke methoden waarbij met willekeurige resp. ‘geneste’ steekproeven wordt gewerkt. Het gemiddelde van de steekproef resultaten is een schatting van de marginal likelihood.
Variationele inferentie
Dit is een techniek waarbij geprobeerd wordt om de complexe posterior-verdeling te benaderen met eenvoudigere verdelingen. Binnen een zogenoemde variationele familie van verdelingen zoek je de verdeling die het dichtst bij de ‘echte’ posterior verdeling ligt, die meer eenvoudige verdeling gebruik je vervolgens om een schatting van de marginal likelihood te maken.

Variationele inferentie is een methode die niet specifiek is voor active inference, maar algemeen wordt toegepast bij machine learning in de context van generatieve modellen. En dan vooral in situaties waarin data moeilijk te verzamelen of inzichtelijk te maken zijn, maar waar het van belang is om iets te kunnen zeggen over de (on)zekerheid van wat de machine leert. Je wilt dat liever niet laten afhangen van de hidden layers waarin gewichten en biases worden ‘geleerd’.

Als ik Friston cs (Friston 2022) goed interpreteer is variationele inferentie de manier waarop zij met het berekenbaarheidsprobleem om gaan. Uiteindelijk leidt die methode tot de operationalisering van kernbegrippen uit de theorie, met name die rond het minimaliseren van free energy als basis voor het kiezen van acties, planning en besluitvorming door een intelligent agent. Dat is voor volgende berichten.