Ben ik wel Bayesiaans genoeg?
Mijnheer Van Dijk was geen Bayesiaan, anders had hij nog wel een keer gekeken misschien. Nu staat er op de fictieve grafsteen van de even fictieve man:
Hier ligt Van Dijk, hij had gelijk, hij kwam van rechts.
Ik moet eerlijk bekennen dat ik tot voor kort niet had gehoord dat er onder statistici twee kampen bestaan: de Bayesianen en de frequentisten. Het is wellicht overdreven om over kampen te spreken omdat de verschillende manieren van beschouwen ook complementair kunnen zijn en als verschillende gereedschappen kunnen worden ingezet. Onder de gereedschappen liggen echter ook principieel verschillende opvattingen over wetenschap en de beschouwing van de wereld.
NB De verschillen zijn grimmiger geworden tijdens de zg. replicatiecrisis in de psychologie en in de sociale wetenschappen toen bleek dat resultaten van gepubliceerde onderzoeken, ook die met veel impact, niet altijd reproduceerbaar waren. De oorzaak lag bij het inzetten van het frequentistische gereedschap ‘p-waarde’. Veel artikelen zijn toen teruggetrokken.
NB De afbeelding is ter verluchtiging en wordt in het bericht niet gebruikt.
Hoe sta je er zelf in?
We doen een test, een gedachtenexperiment (maar je zou het ook kunnen uitvoeren). Ik heb hier een normale euromunt, met twee verschillende kanten, kop resp. munt. Als ik die euro op gooi, wat is dan de kans dat na de landing kop boven ligt? Ik hoor je zeggen, en zeg het je na: 50%.
Nu gooi ik die munt ook echt op, en vang hem op in mijn hand, afgedekt met mijn andere hand — zoals dat vaak gaat bij tossen.
Ik kijk nog even niet en laat het jou ook niet zien – en stel nogmaals de vraag:
wat is de kans dat kop boven ligt?
- Zeg jij: ja dat is natuurlijk nog steeds 50%. Er is voor mij toch niets veranderd?
- Of zeg je: wat een onzin vraag. De munt is geland dus ligt met kop boven of onder, er is geen sprake meer van kans maar van zekerheid — alleen ken ik die nog niet.
Het eerste antwoord is dat van een Bayesiaan, die gaat uit van eigen perspectief, van een subjectieve waarneming van de werkelijkheid zo je wilt. Het tweede antwoord is typisch voor de frequentist: alleen de buitenwereld telt, en de objectief vaststelbare zaken daar – ook al ken je die soms (nog) niet.
Drie deuren probleem
Het drie-deuren-probleem, ook bekend als het Monty Hall probleem, test je intuïtie op het gebied van het inschatten van waarschijnlijkheden. Een klassieker waarvan de oplossing veel rumoer opleverde, zelfs bij wiskundigen.
Waar gaat het over? Jij bent deelnemer aan een spelshow op televisie waarin een auto te winnen is. De oerversie komt uit het programma Let’s Make a Deal dat van 1963-1977 werd uitgezonden met presentator Monty Hall.
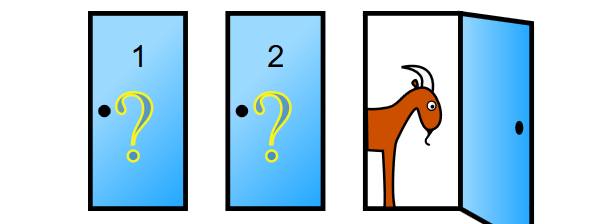
Je staat op het podium waar ook drie gesloten deuren zijn. De presentator vertelt je dat er achter één van de deuren een nieuwe auto staat, of in elk geval de sleutels, achter de andere deuren staat een geit. Je mag een deur kiezen en wat er achter staat mag je houden. Misschien ga je met een mooie auto naar huis, misschien met een geit – het hangt van je keuze af.
Kies een deur, zegt de presentator, en ga er alvast voor staan. Dan zal ik de deur openen en weet je wat je gewonnen hebt. Je kiest een deur, zeg deur 1, en gaat er staan. De presentator komt aanlopen om het geheim te onthullen, maar houdt de pas even in en zegt dat hij het nog wat spannender wil maken. Hij zal eerst een van de andere deuren openen en je laten zien wat er achter staat, daarna mag je nog van keuze veranderen! Hij opent deur 3, en zie – daar staat een geit.
Wat nu? Je hebt deur 1 gekozen, maar de presentator zegt dat je naar deur 2 mag overstappen. Maakt het wat uit? Is het verstandig om te switchen of juist te blijven staan?
Een frequentistische kandidaat zal zeggen: het maakt niks uit – er zijn nog twee deuren over, achter een deur staat een auto, achter de andere een geit. Eerst was mijn kans om goed te raden 1/3, nu er een deur afvalt is het fifty-fifty geworden, ik kan net zo goed blijven staan.
Een Bayesiaanse kandidaat heeft een andere redenering en zegt: met elke deur die ik aan het begin kies heb ik kans 1/3 dat ik de auto win. Anders gezegd: de kans is 2/3 dat ik verlies omdat de auto achter een van de twee andere deuren staat. De presentator weet natuurlijk waar de auto staat en opent een deur met een geit. Er is achter de deuren zelf niets gebeurd, dus de kans dat de auto achter de twee niet door mij gekozen deuren staat is 2/3 gebleven.
Omdat een van de twee niet gekozen deuren geopend is, in dit geval deur 3, weet ik nu zeker dat áls de auto niet achter mijn deur 1 staat hij wel achter deur 2 moet staan. De kans dat mijn eigen deur de goede is blijft 1/3, maar de kans dat de auto achter deur 2 staat is 2/3 geworden. Ik verander dus mijn keuze naar deur 2 en vergroot mijn kans op de auto naar 2/3.
Wat is de crux in de Bayesiaanse redenering? Door het openen van een deur heb ik nieuwe informatie over ‘de wereld’ gekregen. Daar waar in het begin, a priori, de kans op de auto voor elke deur 1/3 was, is ná de opening, a posteriori, de kans van een van de deuren veranderd (verdubbeld). Ik pas mijn wereldbeeld daar op aan.
NB Merk op dat de aanname dat de presentator zijn kennis over waar de auto staat gebruikt om een deur te kiezen hier essentieel is. De aanvullende informatie is het gevolg van de restricted choice die de presentator heeft. Als de presentator met een munt of dobbelsteen zou kiezen, zou je geen aanvullende informatie over de wereld hebben gekregen, dan was immers niet uitgesloten geweest dat hij jouw deur of de deur met de auto zou openen.
Test resultaat
Stel dat je om wat voor reden dan ook een medische diagnose test hebt gedaan om te kijken of je de ziekte Z hebt. De dokter heeft je verteld dat Z op dit moment voorkomt bij 0,1% van de bevolkingsgroep waar je bij hoort. De test is heel betrouwbaar zegt ze, met een ‘betrouwbaarheid’ van 99%. Daarmee wordt bedoeld dat van alle mensen die een positieve uitslag kregen waarmee Z wordt aangetoond, 99% de ziekte ook daadwerkelijk heeft.
Een paar dagen later wordt je gebeld: slecht nieuws – de test heeft een positieve uitslag laten zien. Het lijkt erop dat je inderdaad Z hebt opgelopen.
Het is echt geen goed bericht, maar zit je bij de pakken neer en denk je dat het voor 99% zeker is dat je Z hebt? Of ga je er nog op een Bayesiaanse manier naar kijken?
In het plaatje geeft de ene rode stip in het veld van 1.000 stippen de genoemde 0,1% weer – 1 op de 1.000 mensen heeft Z. Misschien ben jij die rode stip.
De betrouwbaarheid van de test is 99%. Dat wil zeggen dat in 1% van de gevallen de test wel positief uitsloeg maar dat de geteste persoon Z niet heeft.
Die zogenoemde ‘false positives’ zijn de blauwe cellen in het plaatje.
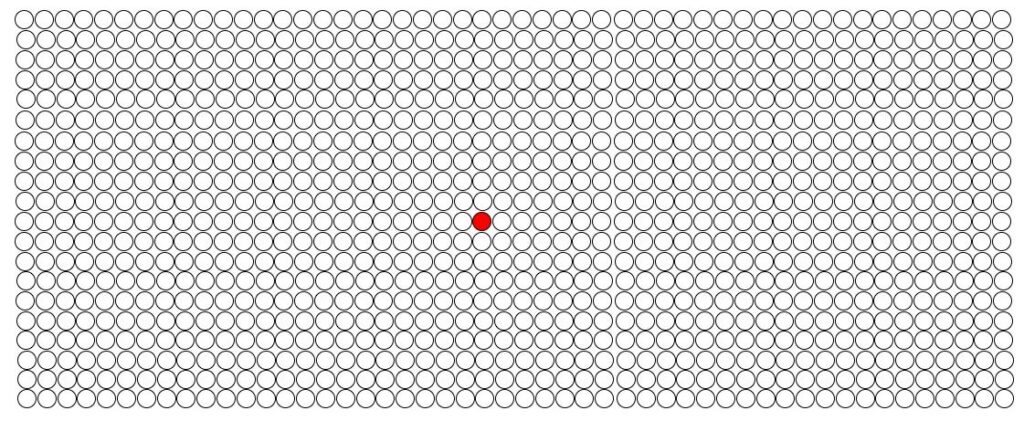
Op de groep van 1.000 geteste personen zijn er dus 11 met een positieve uitslag. Jij bent daar bij, maar heb je ook daadwerkelijk Z?
In deze manier van kijken is de kans dat jij Z hebt dus gelijk aan 1 op 11, zeg maar 9%. Nog steeds slecht nieuws, maar toch minder dramatisch dan de 99% die je eerst dacht.
Het medische diagnose voorbeeld is in de literatuur een soort standaard geworden om de stelling (en formule) van Bayes toe te lichten. Daar wordt meestal gerekend in plaats van getekend. Dat ga ik in een volgend bericht ook doen, nadat ik de formule die bij de stelling hoort aannemelijk heb proberen te maken.